| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 과잉캐리어
- EE204
- 공핍영역 넓이
- PN diode
- minority carrier
- SVP
- 삼성전자
- PN junction
- 반도체소자
- 전자농도
- 반도체이론
- 반도체
- 삼성전자DS
- 맛집
- 취업준비
- 공간 전하 영역
- 물리전자개론
- 합격후기
- pn접합
- 홀
- 삼성면접
- Lifetime
- 반도체연구소
- 점진적 도핑
- DEPLETION REGION
- 반도체 이론
- 공핍영역
- 반도체 소자
- 당일치기
- 무한리필
- Today
- Total
쿠크다스 멜랑쥬
물리전자개론#4-1 평형상태의 캐리어 농도, 진성반도체, 페르미 에너지 레벨 위치, 도핑, 이온화 에너지 본문
4.0 | PREVIEW
In this chapter, we will:
■ Derive the thermal-equilibrium concentrations of electrons and holes in a semiconductor as a function of the Fermi energy level.
■ Discuss the process by which the properties of a semiconductor material can be favorably altered by adding specific impurity atoms to the semiconductor.
■ Determine the thermal-equilibrium concentrations of electrons and holes in a semiconductor as a function of the concentration of dopant atoms added to the semiconductor.
■ Determine the position of the Fermi energy level as a function of the concentrations of dopant atoms added to the semiconductor.
4단원에서는 평형상태(equilibrium)에서의 반도체를 살펴볼 것이다. 평형상태의 반도체에서의 전자/정공 농도, 진성/외인성 반도체, 화합물 반도체, 도핑(Doping), 페르미 레벨 등을 배울 것이다.
4.1 | CHARGE CARRIERS IN SEMICONDUCTORS (반도체 내부 캐리어)
전류는 전하의 흐름인데 반도체에서는 두가지 종류의 전하입자가 있다 : 전자(electron)와 정공(hole). 실질적으로 전류에 기여하는 것은 전도대(conduction band)에 있는 전자와 가전자대(valance band)에 있는 정공이다. 우리가 관심있는 것은 반도체에서의 전기적 특성이고 이를 알기 위해서는 전자와 홀의 양을 알아야 한다. 이를 위해서 3단원에서 상태밀도(DOS)와 페르미-디락 분포함수를 배웠는데 이제 이들을 이용해서 '평형상태'에서 전자와 정공이 얼마나 있는지를 수학적으로 구해볼 것이다.
4.1.1 Equilibrium Distribution of Electrons and Holes (평형상태에서의 전자와 정공분포)

전도대에서 전자분포 함수(electron distribution)는 위와 같다. 단위는 \( 갯수/eV\cdot cm^3 \)(입자의 개수 per 단위 에너지 per 단위 부피)임을 유의하자.
비유하자면, 전류밀도(\(n(E)\))는 아파트에 사는 주민의 수라고 하면 아파트 내의 집의 갯수는 상태밀도함수(\(g_c(E)\))이고 집마다 사람이 있을 확률이 페르미-디락 분포함수(\(f_F(E)\))인 것이다. 아파트 마다 집의 갯수, 사람이 살 확률이 다른데 이는 에너지 레벨 (E)에 대한 함수에 해당한다. 이를 전도대 전체 에너지(\(E_c ~ \infty \))에 대해 적분하면 단위 부피당 전자의 개수(= 전자 농도, electron concentration)를 알 수있다.

가전자대에서 정공 분포함수(hole distribution)는 위와 같다. 단위는 전자의 경우와 동일하다. 정공은 전자가 빠져나간 구멍이 입자처럼 행동하는 것이기에 존재확률은 전자가 존재하지 않을 확률과 동일하다. 따라서 \(f_F(E)\) 대신 \(1-f_F(E)\)가 정공의 존재확률이 된다. 여기에 가전자대에서의 상태밀도를 곱하면 정공의 밀도가 된다. 동일하게 모든 에너지 영역에서 적분하면 정공의 농도를 구할 수 있다.
우리는 (열적)평형상태에서의 전자/정공 농도를 알고 싶다. 이를 알기 위해서는 상태밀도 함수와 페르미-디락 분포함수에 대해 알고 있어야 한다. 우리가 상태밀도 함수의 모든 항을 알고 있는 값인 반면에 페르미-디락 분포함수에서는 페르미 레벨 (\( E_F\))항을 아직 모른다. 따라서 우리는 페르미 레벨 \( E_F\)을 알고 시작해야 한다.


페르미 레벨 \( E_F\)를 논하기 전에, 우선 진성 반도체(intrinsic semiconductor)라는 조건이 필요하다. 진성 반도체는 아무런 불순물과 defects가 없는 순수한 상태의 반도체를 의미한다. 대표적인 예시로 pure Si,Ge 등이 있다. 먼저 T=0K 환경에서 Intrinsic Si를 보자. \(E_c\)에는 아무런 전자가 없고 \(E_v\)에는 모두 전자로 채워져 있을 것이다. 그렇다면 \(E_F\)는 전자가 존재할 확률이 0.5인 지점이므로 \(E_c\) 와 \(E_v\) 그 사이 어딘가에 있다는 것을 추측할 수 있다. 일반적으로 우리는 (전자와 정공의 유효질량을 동일하게 가정한다면) 그 중간 지점을 \(E_F\)라고 가정한다. (정확히는 intrinsic상태의 페르미 레벨로 \(E_Fi\) 라고 표기한다. \(E_F\)는 에너지를 대변하는 요소중 하나라 상황에 따라 위치가 달라진다.)
지난 시간에 E에 따른 상태밀도 함수와 페르미 디락 분포함수를 배웠다(#3-3 Introduction to the QuantumTheory of Solids). 이제 이 둘을 곱하면 전자(또는 정공) 농도가 되므로 이를 그래프에서 합쳐보자.

왼쪽 그래프의 우측에 색칠되어있는 두개의 그래프는 DOS와 FD 분포함수의 곱이고 이들의 영역(전 에너지 영역에서의 적분)이 각 입자의 농도를 의미한다. 여기서 두개의 그래프가 정확히 대칭은 아니다. 전자와 정공의 유효질량이 다르기 때문에 미세한 차이가 있지만 만약 두 값을 같다고 가정하면 두 그래프는 대칭일 것이다.
4.1.2 The n0 and p0 Equations (평형상태에서의 캐리어 농도 곱)
위 그래프에서 구했던 농도들을 식으로 나타내면 다음과 같다.
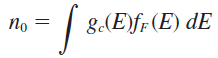
이 식을 조금더 정확히 풀어쓰면, (페르미-디락 분포함수는 볼츠만 근사)
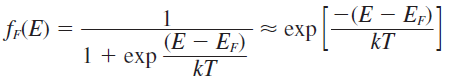
exp항이 충분히 작은 경우(온도가 충분히 높거나 E가 큰 경우), FD 함수는 다음과 같이 볼츠만 함수형태로 근사 가능하다.
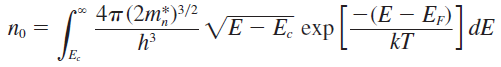
식의 간편화를 위해 \(\eta =\frac{E-E_c}{kT}\) 라는 변수를 정의한 후 다시 정리하면,
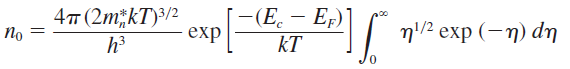
여기서 우측의 적분항은 수학적으로 \(\frac{1}{2}\sqrt{\pi} \) 값을 가진다.
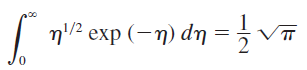
따라서 식을 정리하면 결국 전자의 농도는 다음과 같이 표현된다.
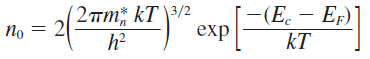
이때 우측은 기존의 FD함수 형태를 가지며 좌측의 항은 (일정 환경이 주어진다면) 상수값을 가지기 때문에 간편화를 위해 \(N_c\)로 표현하고 이를 전도대에서의 유효 상태 밀도함수(effective density of states function in the conduction band) 라고 한다.
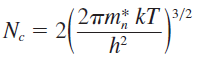
따라서 전자의 농도는 일반적으로 다음과 같이 표현한다. 일반적으로 T=300K에서 \(2.5 \times 10^{19} cm^{-3}\)의 값을 갖는다. 온도나 유효질량에 따른 함수임을 잊지말자.
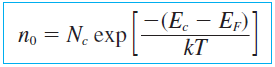
같은 방식으로, 가전자대에서 정공의 농도는 다음과 같다. 다만 페르미 에너지와 band energy의 부호만 조심하자.

4.1.3 The Intrinsic Carrier Concentration (진성 반도체 캐리어 농도)
진성 반도체에서는 외부적 요인이 아무것도 없는, 순수한 상태의 반도체이기 때문에 전도대의 전자만큼 가전자대의 정공이 생성된다. 따라서 진성반도체의 전자와 정공농도를 \(n_i\) 와 \(p_i\)라고 하면 \(n_i = p_i\) 이다. 일반적으로 \(n_i\)로 통징한다. 이때의 페르미 에너지 레벨 역시 \(E_F \)가 아닌 \(E_{Fi}\)로 표기한다.
-\(n_{i}^2\)
위에서 배운 농도식들을 곱하게 되면 다음식처럼 표현할 수 있다.
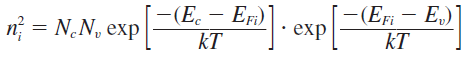
exp항을 합쳐보면 \(E_{Fi}\)항이 소거되고 \( -(E_c - E_v) \)항만 남는데 이 값은 전도대와 가전자대의 에너지 레벨차이(bandgap energy), \(E_{gap} \)으로 주어지는 값이다. 따라서 \( n_{i}^2 \) 값은 (온도와 유효질량이 주어진 상태에서) 상수값을 갖는다.
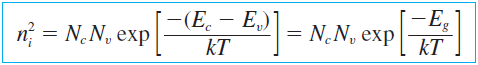
통상적으로 상온(T=300K)에서 진성실리콘은 밴드갭 에너지가 1.12eV, 진성 캐리어 농도 \(n_{i}^2\)는 이론적으로 \(6.95 \times 10^9 cm^{-3}\), 일반적으로 사용되는 값은 \(1.5 \times 10^10 cm^{-3}\) 값을 가진다. 기준값으로 쓸 일이 많으므로 외워두면 좋다.
여기서 "어? 근데 우리는 DOS 구할때 3D 무한 퍼텐셜 우물을 가정했고 유효질량 역시 조금씩 변동이 생겨 N값들에 차이가 생길텐데 위 식의 값을 쓰는게 맞나요?" 라고 할 수 도 있다. 맞는 말이지만 실제값과 이론값의 차이가 크게 나지 않기때문에 사용해도 무방하다.
-온도 의존성
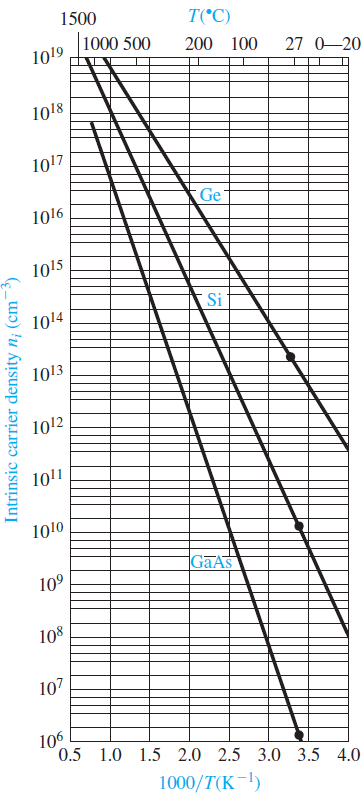
진성 반도체의 캐리어 농도는 온도에 굉장히 민감하다. 다음 그래프는 온도에 대한 캐리어농도에 대한 그래프인데 y축이 로그단위인 것을 감안하면 온도에 따라 굉장히 큰 차이를 보인다는 것을 알 수 있다.
4.1.4 The Intrinsic Fermi-Level Position (\(E_{Fi}\) 위치)
이때까지 우리는 \(E_{Fi}\)가 "대략" 전도대와 가전자대 중간에 위치할 것이라고 가정했다. 하지만 유효질량의 차이때문에 정확히 중간값은 아닐 것이라고 추측할 수 있다. 따라서 \(E_{Fi}\)의 위치를 수학적으로 계산해 볼 것이다.
우선 진성 반도체에서 전자와 정공의 농도는 동일하므로 다음과 같은 식을 쓸 수 있다.
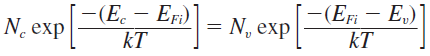
양변에 로그를 취한 후, 우리가 알고자 하는 \(E_{Fi}\)에 대해 정리하면,
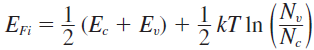
또는, 유효 상태 밀도함수를 더 풀어서 정리하면 다음과 같은 식을 얻을 수 있다.
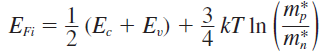
여기서 우변의 왼쪽 항은 전도대와 가전자대의 정중앙 위치(midgap)을 의미한다. 따라서 우리가 이때까지 중간이라고 사용해왔지만 실은 \( \frac{3}{4}kT \ln(\frac{m_p^*}{m_n^*}) \)만큼의 차이가 존재한다. 만약 우리가 전자와 정공의 유효질량을 같다라고 가정하면 ln항이 0이 되어 가정한대로 midgap이 \(E_{Fi}\)와 동일하겠지만 그렇지 않기 때문에 살짝 위치가 달라지게 된다.
4.2 | DOPANT ATOMS AND ENERGY LEVELS (도펀트 원자와 에너지 레벨)
이전까지는 외부 요인이 없는 진성 반도체(intrinsic)만 다루었다면 이제는 외부 요인이 첨가된(도핑된) 외인성 반도체(extrinsic)를 다룰 것이다. 반도체에 다른 원소를 도핑하는 이유는 반도체의 전기적 성질을 조절하기 위함이다.
4.2.1 Qualitative Description (도핑에 대한 간단한 설명)

우리가 흔히 반도체로 사용하는 물질은 Si와 Ge이다. 이들은 모두 14족 원소로 최외각 전자가 4개가 존재하여 다이아몬드 결합구조를 이룬다. 여기에 도핑용으로 사용하는 원소들은 14족이 아닌 13족과 15족원소들 (간단히 3족, 5족)을 사용한다. 이들은 기존의 결합을 이루고 있는 원자들 보다 전자가 1개 적거나 많다. 따라서 도핑 원소가 결정을 이루게 되면 도핑 원자 하나당 전자 한개가 부족하거나 과잉된다는 말이다. 이는 곧 정공과 전자의 생성을 의미하게 되고 이는 전기적 성질에 영향을 미치게 된다.
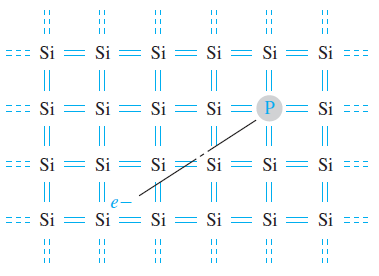
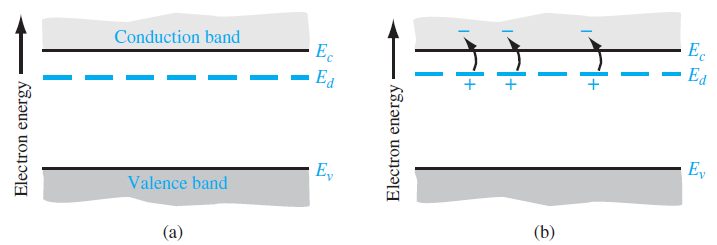
조금 더 상세히 살펴보자. 진성 실리콘 반도체에 인(P,15족)원자가 dopant로 들어왔다. 인은 기존의 Si 자리중 하나를 차지하여 결정구조를 유지하는데 최외각 전자 1개는 인접원자와 공유결합에 참여하지 않게 된다. 이러한 전자는 전도대로 가기 위해 기존의 공유결합에 해당하는 에너지가 불필요하다. 밴드로 표현하자면 dopant의 전자는 기존의 가전자대보다 훨씬 위에 에너지 레벨이 존재하게 되는 것이다. 이렇게 15족으로 도핑되어 전자가 과잉된 반도체를 n-type 반도체라고 한다. 그리고 n-type 반도체를 만들게 하는 impurity는 전자를 기여해서 donor라고 한다.
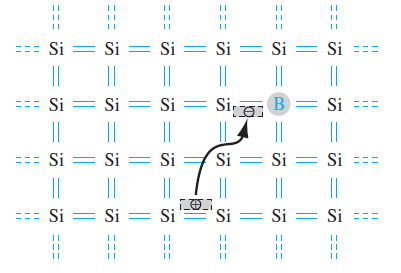
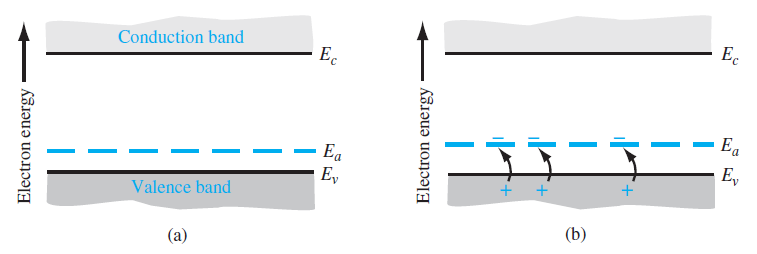
그렇다면 13족 원자를 도펀트로 주입하면 어떤 결과가 나올까? 전자를 정공에 대입하면 동일한 결과를 보인다. 여기서는 해당 도펀트 원자는 하나의 공유결합이 부족하기 때문에 주변의 전자가 해당 결합을 채우기 위해 이동하게 된다. 따라서 이 경우 정공이 생기기 쉬워지는 효과가 나타나고 이는 에너지 밴드상에서 가전자대 근처에 에너지 레벨이 존재하게 된다. 이렇게 13족으로 도핑되어 정공이 전자보다 많게 되는 반도체는 p-type 반도체라고 한다. 그리고 이때 impurity atom은 전자를 수용하기 때문에 acceptor라고 한다.
4.2.2 Ionization Energy (이온화 에너지)
이제 도펀트를 넣어줄 경우 (n-type의 경우) 전자가 전도대로 가기위해서 얼마만큼의 에너지가 필요한지 궁금해졌다. 도펀트의 원자와 전자간의 거리를 대략 알 수 있으므로 이온화 에너지를 수학적으로 계산할 수 있을 것 같다. 식의 간략화를 위해 보어모형을 가정한다.
이전 단원(물리전자개론#2-3 Introduction to Quantum Mechanics)에서 보어 반지름과 총 에너지에 대해 배웠다.
-일반적으로 전기력과 원심력의 평형에서 시작한다.
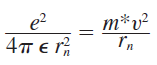
이전 양자역학 단원에서 보어모형의 각운동량은 양자화 되어있다고 배웠다.
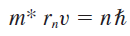
우리는 전자의 속력을 잘 모르니까 위 식에서 v에 대해 정리한 뒤 첫 번째 식에 대입할 것이다. 그 후 반지름 \(r_n \)에 대해 정리하면 다음과 같다. 여기서 각운동량의 양자화에 의해 전자궤도도 양자화 되어있다고 가정하자.
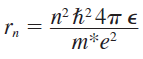
2-3때도 언급했지만 기본상태(진공상태, 불변질량)에서 가장 첫 번째 반지름을 보어 반지름이라고 한다. (불변질량 = 정지질량, 정지상태에서의 전자의 질량) 일반적으로 반지름에 대한 식을 양변 \(a_0\)를 나눠서 normalize한다. 이 식에 원하는 원자의 유전상수(\(\epsilon_r \)), 유효질량 등을 넣어서 계산할 수 있다.
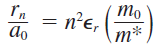
-총 에너지는 역학적 에너지와 위치에너지의 합이다.
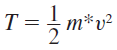
여기서 v를 위에서 각운동량 양자화에 대한 식을 사용하여 치환한 후, 대입하면
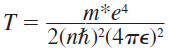
퍼텐셜에너지는 전기력에서의 퍼텐셜 에너지이다. 여기서 r에대한 식을 각운동량 양자화에 대한 식을 사용하여 치환하면,
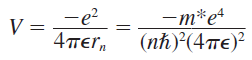
이를 퍼텐셜 에너지와 합하면
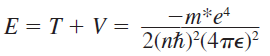
가 된다.
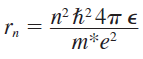
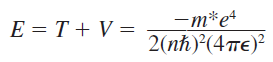
가장 작은 원자인 수소 원자의 이온화 에너지는 -13.6eV이다. 반면 Si의 경우 이온화 에너지는 -25.8meV에 불과하다. Si의 밴드갭 에너지인 1.12eV에 비하면 굉장히 작은 값임을 볼 수 있다. 보통 도핑된 Si나 Ge를 사용하는데 이때 각 dopant에 따른 이온화 에너지는 다음과 같다.
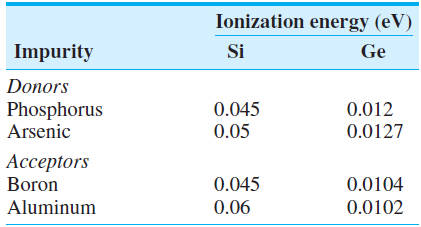
4.2.3 Group III–V Semiconductors
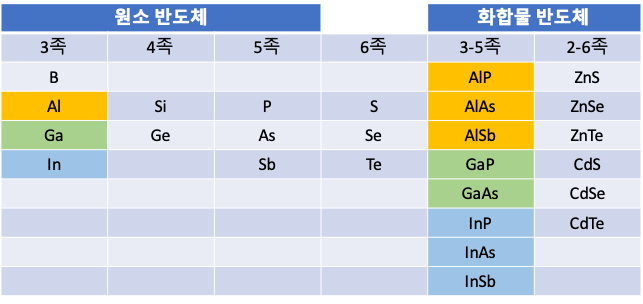
이전까지는 단일 원소로 구성된 반도체-Si,Ge를 배웠지만 이 외에도 3족과 5족의 화합물도 반도체가 될 수 있다. 대표적인 예시로는 GaAs(gallium arsenide), InP(Indium Phosphide)가 있다. 이러한 반도체의 경우 dopant로는 2족, 4족, 6족을 사용할 수 있다. 2족이 3족을 대체하거나 6족이 5족을 대체하는 경우 이전과 같은 원리로 정공과 전자가 생성되는데, 4족의 경우 3족을 대체하는 경우와 5족을 대체하는 경우가 달라지게 되는 양쪽성(amphoteric)을 가지게 된다. GaAs에서 도핑한다고 하면 일반적으로는 Si의 경우 donor(3족 대체)로 활동하고 Ge의 경우 acceptor(5족 대체)로 활동한다.
물리전자개론#4-2 The Semiconductor in Equilibrium 에서 계속
물리전자개론#4-2 The Semiconductor in Equilibrium
4.3 | THE EXTRINSIC SEMICONDUCTOR (외인성 반도체) 우리가 외부 요소가 없는 반도체를 진성반도체(intrinsic semiconductor)라고 했고 평형상태에서 진성반도체를 살펴보았다. 실제 반도체는 impurity를 추가하여
cucudasdiary.tistory.com
이전글
물리전자개론#3-3 Introduction to the Quantum Theory of Solids(Density of states at 1D/2D/3D, 통계역학,페르미-디락
3.4 | DENSITY OF STATES FUNCTION 우리는 전류 전압특성을 다루기 위해 우선 전하를 가지는 입자들의 분포(charge carrier distribution), 또는 전자와 정공의 분포를 알고 싶다. 이를 알기 위해서는 Density of State
cucudasdiary.tistory.com




