| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- minority carrier
- Lifetime
- 반도체 이론
- 전자농도
- PN junction
- 공핍영역
- 반도체이론
- SVP
- 점진적 도핑
- 공간 전하 영역
- EE204
- 반도체연구소
- 물리전자개론
- DEPLETION REGION
- 취업준비
- 맛집
- 홀
- PN diode
- 삼성면접
- 합격후기
- 반도체소자
- 삼성전자
- pn접합
- 반도체
- 삼성전자DS
- 공핍영역 넓이
- 무한리필
- 당일치기
- 과잉캐리어
- 반도체 소자
- Today
- Total
쿠크다스 멜랑쥬
물리전자개론#3-1 Introduction to the Quantum Theory of Solids(에너지 밴드 이론, 크로니그-페니 모델,에너지 밴드갭,브릴루앙 영역) 본문
물리전자개론#3-1 Introduction to the Quantum Theory of Solids(에너지 밴드 이론, 크로니그-페니 모델,에너지 밴드갭,브릴루앙 영역)
쿠크다스 멜랑쥬 2022. 9. 20. 22:59
Chapter 3. Introduction to the Quantum Theory of Solids
<preview>
(at Single crystal)
-Describe forbidden electron energy bands(금지대), conduction and valence energy bands(전도대, 가전자대)
-E-k diagram(에너지-모멘텀), Direct gap, Indirect gap
-effective mass of electron & hole (유효질량)
-DOS(Density Of States,상태밀도)
-Fermi-Dirac 확률 함수
3.1 | ALLOWED AND FORBIDDEN ENERGY BANDS
지난 시간에 1전자 원자(H atom)에서 전자의 에너지는 이산적으로 분포(양자화)한다는 것을 알아냈다. (https://cucudasdiary.tistory.com/8 참고) 이는 곧 전자의 에너지가 존재할 수 있는 곳과 없는 곳을 나타내고 후에 이 에너지 대역을 energy band라고 한다.
3.1.1 Formation of Energy Bands
결정은 수많은 원자간의 상호작용이지만 전자의 에너지를 파악하기에는 불가능하므로 이를 간단히 보기 위해서 두 개의 수소원자가 접근하는 단순한 모형을 생각해보자.

원자가 움직이고 있는 반지름 방향으로의 축(radial axis, 그림에서 x축)에서의 전자의 상호작용을 분석해보자. 축 방향에서의 전자의 확률함수는 다음과 같다.
(\( \psi(r,\theta ,\phi)=R(r)\Theta(\theta)\Phi(\phi) \) 에서 R(r)에 대한 확률함수, \(\psi _{100}=\frac{1}{\sqrt{\pi} }(\frac{1}{a_0})^\frac{2}{3}e^{-\frac{r}{a_0}}\))

두 개의 원자 모두 같은 전자 확률함수를 가지므로 위 모델에 대한 전자의 확률함수는 다음과 같게 된다.

확률함수가 겹치는 것은 전자가 서로 상호작용을 한다는 것을 의미한다. 페르미온 입자는 파울리 배타원리를 충족하므로 겹치는 부분에서 전자들은 서로 다른 에너지 상태를 가져야 한다. 따라서 겹치는 부분에서의 전자 에너지는 다음과 같이 분리된다. (하나는 bonding, 다른 하나는 anti-bonding 상태로 기존 에너지 레벨보다 낮거나 높은 상태로 분리된다.)

일반적인 결정구조는 반복되는 원자들의 집합이기 때문에 하나의 전자에 대해 수많은 전자와의 상호작용이 일어나게 된다. 따라서 파울리 배타원리를 적용하면, 전자의 에너지 레벨은 다음 그림과 같이 다른 전자들과의 상호작용하는 만큼 분리된다.

다만, 실생활에서는 결정 내 전자의 갯수는 \( 10^{20} \)이상으로 많이 존재하므로 각 에너지 레벨간 차이는 연속이라 해도 될 만큼 작아지게 된다. 예를 들어 허용된 에너지 레벨의 높이가 1eV라면 그 속의 에너지 레벨간 격차는 \( 10^{-20} eV\)이하로 매우 작아지게 된다. 따라서 고전물리에서는 에너지가 연속적인 특성을 갖는다(quasi-continuous energy distribution).
조금 더 일반적인 경우로, 같은 상황에서 n=3인 원자를 생각해보자(대표적으로 Si, 전자 껍질이 3개).
이 경우 외각에 위치한 전자 (n=3인 전자) 부터 가장 안쪽의 전자까지 (n=1인 전자) 차례대로 이웃한 원자의 전자와 상호작용을 하기 시작할 것이다. n=3인 전자들의 상호작용을 고려해보면, 전자들 중에서 원자간 거리(interatomic distance)가 가장 멀 때부터 상호작용을 시작하며 전자의 개수가 많으므로 energy band내 전자의 에너지 레벨이 많다. 이를 거리-에너지 그래프로 그려보면 다음과 같다.
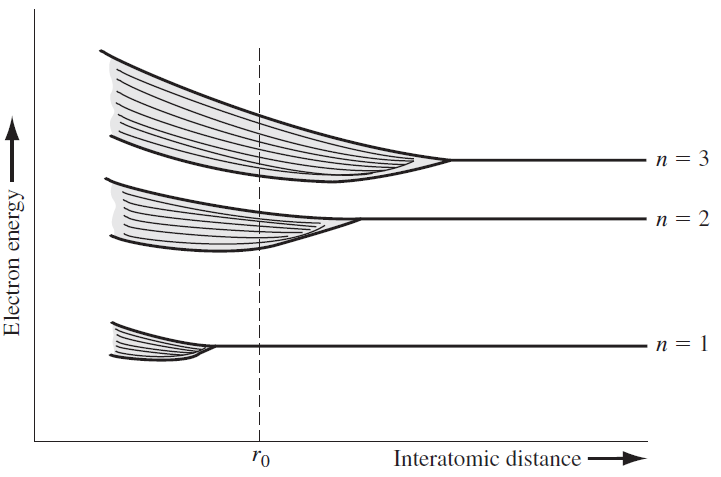
반도체 주재료인 Si(14, \(3s^2 3p^2\) )를 예시로 전자의 상태를 조금 더 자세히 살펴보자. 고등학교때 오비탈을 배울때 같은 주양자수 n을 갖고 있더라도 부양자수가 다른 경우 전자의 분포가 달라짐에 대해 배웠다(s, p, d ....).
Si의 경우 3s 오비탈에 2개, 3p 오비탈에 2개의 전자를 가지고 있고 이 둘의 에너지 차이가 존재한다. 거리가 점점 좁혀져, n=3 전자만 상호작용 하는 거리에 있고 온도가 매우 낮아 모두 bonding 상태에 있다고 가정한다. 3s는 2개의 states, 3p는 6개의 states를 갖어 총 8개의 states를 갖는데 이 중 절반인 4개의 states가 bonding states로 낮은 에너지 레벨을 갖고 나머지 4개는 anti-bonding states로 높은 에너지 레벨을 갖게 된다(chemical bonding theory 참고). 따라서 거리-에너지 그래프는 다음과 같아진다.

(T=0K) 이때, bonding energy band (valence band)와 anti-bonding energy band(conduction band)간 에너지가 존재할 수 없는 구간이 존재하는데 이 구간을 Forbidden energy band, 금지대라고 하며 크기를 \( E_{g} \)(Bandgap energy)로 표기한다.
위 그래프의 개형이 왜 저렇게 되는지에 대한 설명은 여러 모델이 존재하는데 가장 유명한 모델 중 하나가 Kronig-Penny model(k-p model)이다. (다른 이론으로는 Tight binding model, SSH model 등이 있다)
*3.1.2 The Kronig-Penny Model
Kronig-Penny Model의 요점은 '결정(crystal)속 전자는 존재확률이 0인 금지대(forbidden band)가 존재하고 허용된 에너지 밴드에만 존재한다'이고 동시에 위 그래프의 개형을 설명하는 것이다.
Model의 간소화를 위해 potential well이 존재하는(\( E < V_0 \)) 1차원상 1전자 원자 결정에서 슈뢰딩거 방정식의 해답을 찾는다. 우선 '결정'이므로 Bloch theorem(블로흐 정리)이 성립한다. (Bloch theorem: periodic potential energy U(r) = U(r+T), lattice periodic function \(u_{k}(r)= u_{k}(r+R)=\sum^G a_{G}e^{iGr} \) ) 이때 파동함수는 다음과 같다
$$ \psi(x) = u(x)e^{jkx} $$
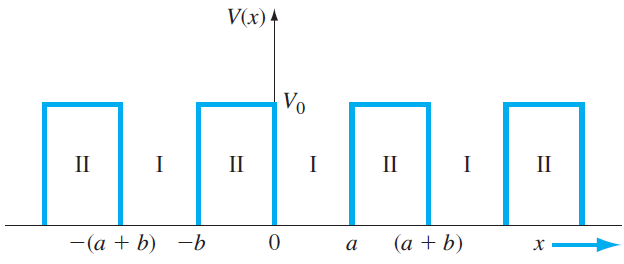
원자에서 위치에 대한 전자의 potential function을 그려보면 첫번째 그림과 같이 된다. 다만 결정구조이므로 동일한 구조의 potential function이 반복되고 있으며 (2번째 그림) 이를 합쳐서 결과만 보면 3번째 그림과 같은 potential function을 갖게 된다.
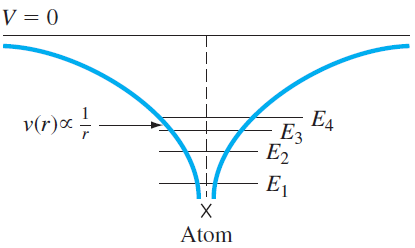
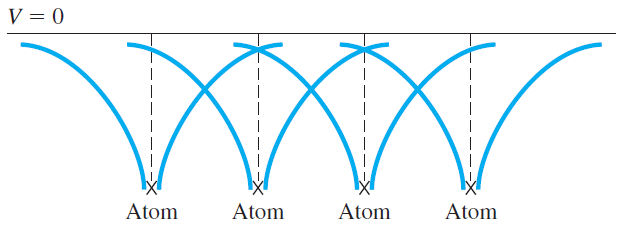
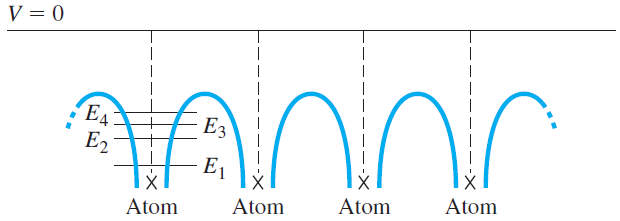
이를 potential에 따른 영역별로 구분하면 다음과 같이 I, II region으로 구분 가능하다.
Chapter 2에서 위와 같은 구조에 대한 슈뢰딩거 방정식의 해는 다음과 같았다.
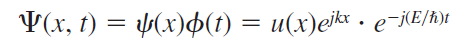
이제 여기서 각 영역에 대해 boundary condition을 적용하여 슈뢰딩거 방정식의 해를 구해보면 다음과 같이 구할 수 있다.(그러나 일부 assumtion 존재; let the potential barrier width b → 0 and the barrier height V 0 → infinite , but such that the product bV =0 remains fi nite.) 이때 \( \alpha \)는 상수, a는 radial distance를 의미한다.
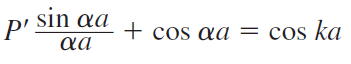
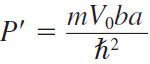
(자세한 유도과정은 다음 링크를 참고)
https://universics.tistory.com/41
에너지 밴드갭이 생기는 이유 (1)
Kronig-Penney model (1) 2012년 11월 14일 수요일 오전 5:06 오늘은 특별부록이예요 ~~^^ 제 인생 최악의 노가다를 공개하겠습니다. 반도체를 공부하다보면 에너지 밴드랑 밴드갭이 나오고 반도체들은
universics.tistory.com
좌변의 P'항과 cos항을 그래프로 그려보면,
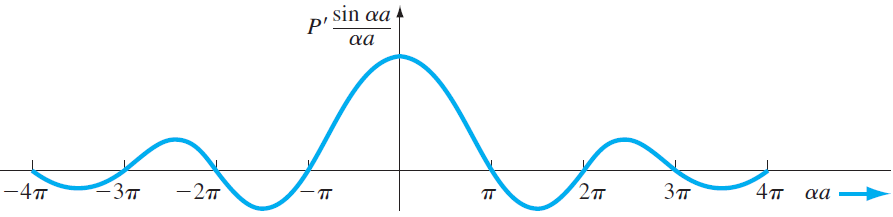

두개의 항의 합을 \( f(\alpha a) \)라고 하자. 그래프로 나타내면 다음과 같다.

근데 이 값은 우변의 cos(ka)와 동치이다. cos함수 특성상 y축 값이 1을 넘지 못하므로 가능한 값들은 그림에서 파랗게 칠해진 부분만 가능하다. 즉, cos(ka)에서 ka값이 양자화 되어있다. ka값은 곧 E와 직접적인 연관이 있으므로 전자가 존재할 수 있는 구간과 없는 구간이 양자화 되어있음을 알 수 있다. 이는 곧 energy band와 forbidden energy band에 대한 설명이다.
이를 E-k diagram으로 표현한다면 다음과 같은 형태를 보인다.
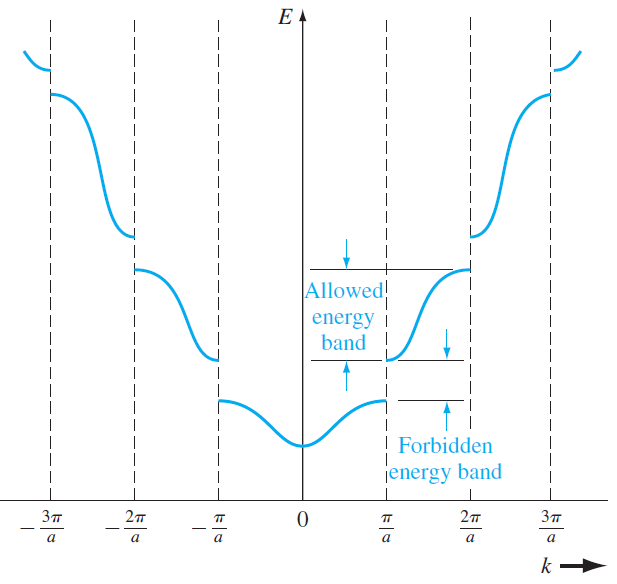
이는 '하나'의 1전자 원자에 대한 전자의 E-k diagram이다. 우리는 지금 결정을 다루고 있으므로 근처의 전자의 E-k diagram도 고려해야한다. 결정이므로 모두 동일한 E-k diagram을 갖는다고 가정할 수 있고 모든 원자의 전자의 E-k diagram을 고려했다고 생각해보자. 그러면 하나의 원자에 해당하는 k( \( -\pi /a < k < \pi /a\) )에 대한 E-k diagram은 다음과 같이 그릴 수 있다.
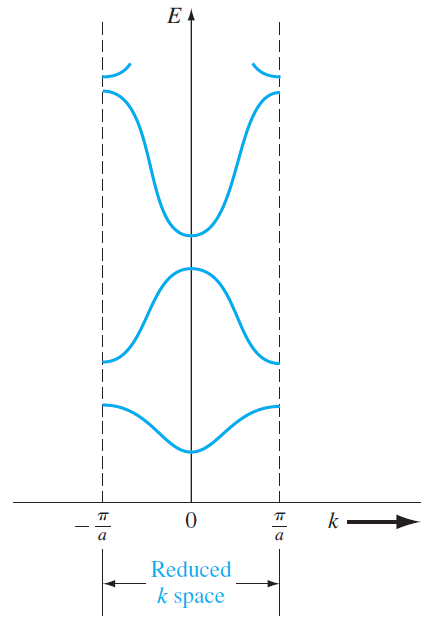
이때 이 영역을 (first) Brillouin zone(브릴루앙 영역)이라고 하고 결정구조의 기본이 되는 영역이다. (나중에 3차원 영역에서도 Brillouin zone과 더불어 irreducible wedge, dgree of symmetry, 등에도 꾸준히 나오는 개념이다.)
다음글:
물리전자개론#3-2 Introduction to the QuantumTheory of Solids
물리전자개론#3-2 Introduction to the QuantumTheory of Solids
3.2 | ELECTRICAL CONDUCTION IN SOLIDS 우리는 기본적으로 반도체 물질에서의 전류-전압특성을 알아보는 것이 목표이다. 따라서 이전 강의에서 배웠던 Band theory를 사용하여 전자의 움직임 부터 알아볼 것
cucudasdiary.tistory.com
이전글:
물리전자개론#2-3 Introduction to Quantum Mechanics(전자의 파동함수,보어모형)
물리전자개론#2-3 Introduction to Quantum Mechanics
EXTENSIONS OF THE WAVE THEORY TO ATOMS 앞으로 결정 원자 내의 전자의 움직임을 파악하여야 한다. 그전에 편의를 위해 1전자 원자(ex) 수소원자) 시스템에서 앞에서 배운 양자역학적 내용을 적용하여 전자
cucudasdiary.tistory.com




