| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 홀
- 맛집
- 공핍영역 넓이
- 공간 전하 영역
- 삼성면접
- 취업준비
- 전자농도
- pn접합
- 반도체 이론
- SVP
- 무한리필
- 삼성전자
- 삼성전자DS
- 점진적 도핑
- PN junction
- EE204
- 과잉캐리어
- 반도체 소자
- DEPLETION REGION
- Lifetime
- 합격후기
- 반도체연구소
- 반도체소자
- minority carrier
- 반도체
- 반도체이론
- 공핍영역
- 당일치기
- 물리전자개론
- PN diode
- Today
- Total
쿠크다스 멜랑쥬
물리전자개론#2-3 Introduction to Quantum Mechanics(전자의 파동함수,보어모형) 본문
EXTENSIONS OF THE WAVE THEORY TO ATOMS
앞으로 결정 원자 내의 전자의 움직임을 파악하여야 한다. 그전에 편의를 위해 1전자 원자(ex) 수소원자) 시스템에서 앞에서 배운 양자역학적 내용을 적용하여 전자의 파동함수를 알아볼 것이다.

위 모델에서 전자-원자핵 시스템에서의 슈뢰딩거 방정식을 세워보자. 구 형태이기 때문에 구좌표계에서의 3차원 슈뢰딩거 방정식을 세운다.편의를 위해 time-independent를 가정한다.
$$ \bigtriangledown^2\psi(r,\theta ,\phi) +\frac{2m_0}{\hbar^2}(E-V_0(r))\psi(r,\theta ,\phi)=0 \\$$
*미적분학2 시간에 배운 구좌표계에서의 라플라시안은 다음과 같다.

*전기자기학 시간에서 배운 potential energy function은 다음과 같다.
$$ V(r)=\frac{-e^2}{4\pi\epsilon_0 r} $$
각 dimension(\(r,\theta , \phi \) )가 독립적이라고 가정하여 변수분리를 사용한다.
$$ \psi(r,\theta ,\phi)=R(r)\Theta(\theta)\Phi(\phi) $$
위 파동함수를 슈뢰딩거 방정식에 대입한 후 식을 전개하면,
$$ \frac{\mathrm{sin^2}\theta}{R}\frac{\partial }{\partial r}(r^2\frac{\partial R}{\partial r})+\frac{1}{\Phi}\frac{\partial ^2\Phi}{\partial \phi^2}+\frac{\mathrm{sin}\theta}{\Theta}\frac{\partial }{\partial \theta}(\mathrm{sin}\theta\frac{\partial \Theta}{\partial \theta})+r^2\mathrm{sin^2}\theta\frac{2m_0}{\hbar^2}(E-V)=0 $$
이때 각 항들에 대해 변수분리 상수를 적용한다. 임의로 r은 n, \(\phi \)는 m, \( \theta\)는 l라는 변수분리 상수를 할당한다. wave function은 single valued이어야 한다고 했기 때문에 각 상수들은 정수값을 갖게 된다. 이 값들이 우리가 고등학교때 배웠던 양자수에 해당한다. 거리에 해당하는 n은 주양자수, l은 방위양자수(부양자수 또는 각운동량 양자수), m은 자기양자수이며 추가적으로 전자의 spin에 해당하는 spin 양자수 까지 해서 4가지 양자수가 존재한다. 주양자수 n은 에너지 준위를 결정하고 이에 해당하는 에너지 준위는 다음과 같다.
$$ E_n=\frac{-m_0e^4}{(4\pi\epsilon_0)^2 2\hbar^2n^2} $$
보어 모형(Bohr Model)
닐스 보어가 제시한 수소원자 모델은 전자의 궤도가 존재하는데(n=1,2,3...) 이 궤도에서 1.전자는 정상파 형태로 존재하며(stationary orbit) 2.궤도간 전자의 이동에서 전자는 빛을 흡수 또는 방출한다. (정상파로 존재해야 closed loop 내에서 상쇄되지 않고 파동이 살아남을 수 있다)
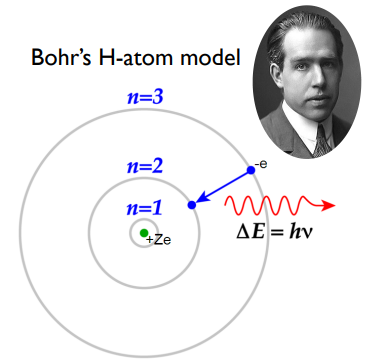
따라서 보어모형에서 각운동량은 궤도에 따라 일정하고 양자화 되어있다.
$$ L_n=mvr=n\hbar $$
이를 기반으로 보어 모형을 해석해보자. 원자핵과 전자간 쿨롱힘은 원운동하는 입자의 원심력과 동일하다.
$$ \frac{1}{4\pi\epsilon_0}\frac{e^2}{r^2}=\frac{mv^2}{r}=\frac{n\hbar v}{r^2}$$
이 식에 각운동량 양자화 식을 적용하면 속력을 알 수 있고 속력을 다시 원 식에 대입하면 원자핵으로부터의 전자의 거리를 구할 수 있다.
$$ r_n=\frac{n^2\epsilon_0\hbar^2}{me^2\pi}=n^2a_B $$
\( a_B \)는 상수로 Bohr radius라고 하며 0.53A의 길이값을 갖는다.
총에너지 E=T+V (운동에너지 + 위치에너지)를 위에서 구한 값들로 구하면 다음과 같이 표현할 수 있다.
$$ E_n = - \frac{13.6}{n^2}eV $$
이 역시 에너지는 n에 따라 양자화 되어있음을 확인할 수 있다.
다음글:
물리전자개론#3-1 Introduction to the QuantumTheory of Solids
물리전자개론#3-1 Introduction to the QuantumTheory of Solids
Chapter 3. Introduction to the Quantum Theory of Solids (at Single crystal) -Describe forbidden electron energy bands(금지대), conduction and valence energy bands(전도대, 가전자대) -E-k diagram(에너지-모멘텀), Direct gap, Indirect gap -effe
cucudasdiary.tistory.com
이전글:
물리전자개론#2-2 Introduction to Quantum Mechanics(1차원 슈뢰딩거 방정식, particle in a box, 경계조건)
물리전자개론#2-2 Introduction to Quantum Mechanics
1차원 슈뢰딩거 방정식 $$ \frac{\partial^2 \psi(x) }{\partial x^2}+\frac{2m}{\hbar^{2}}(E-V(x))\psi(x)=0 $$ 를 사용해서 다양한 환경에서 1전자 원자에 적용시켜보겠다. 2.3 APPLICATIONS OF SCHRODINGER’S WAVE EQUATION (A) Free
cucudasdiary.tistory.com



