| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- pn접합
- 공간 전하 영역
- 삼성전자
- 반도체 소자
- 합격후기
- 맛집
- Lifetime
- 삼성면접
- 당일치기
- DEPLETION REGION
- PN diode
- 과잉캐리어
- 점진적 도핑
- 반도체이론
- 반도체연구소
- 반도체 이론
- 반도체소자
- EE204
- 삼성전자DS
- 홀
- PN junction
- 공핍영역
- 물리전자개론
- 반도체
- 공핍영역 넓이
- 취업준비
- SVP
- 무한리필
- 전자농도
- minority carrier
- Today
- Total
쿠크다스 멜랑쥬
물리전자개론#3-3 Introduction to the Quantum Theory of Solids(Density of states at 1D/2D/3D, 통계역학,페르미-디락 함수, 볼츠만 근사) 본문
물리전자개론#3-3 Introduction to the Quantum Theory of Solids(Density of states at 1D/2D/3D, 통계역학,페르미-디락 함수, 볼츠만 근사)
쿠크다스 멜랑쥬 2022. 10. 26. 23:09
3.4 | DENSITY OF STATES FUNCTION
우리는 전류 전압특성을 다루기 위해 우선 전하를 가지는 입자들의 분포(charge carrier distribution), 또는 전자와 정공의 분포를 알고 싶다. 이를 알기 위해서는 Density of State (상태밀도) 와 Fermi-Dirac function (페르미-디락 분포함수)를 알아야 한다. 상태밀도(DOS)는 에너지마다 파울리 배타원리에 의해 입자가 가질 수 있는 상태 수를 부피로 나눈 것(# of states per unit Energy per unit Volume)이고 페르미 디락함수는 전자가 존재할 확률에 대한 함수이다. 비유하자면 어느 아파트 단지에 거주민 수를 알고 싶은데, 상태밀도는 거주할 수 있는 집이고 페르미 디락함수는 집에 사람이 존재할 확률이어서 두 값을 곱하면 거주민 수를 알 수 있는 것이다.
결론적으로 전자,정공 밀도는 왼쪽 식과 같이 구할 수 있고 각 입자에 해당하는 상태밀도함수는 오른쪽 식과 같다.


이제 우리는 이중 DOS에 대한 것을 유도할 것이다. 우선 존재 가능한 states를 구한 후, 해당하는 단위 energy 값과 volume 값을 나눠주면 구할 수 있을 것 같다.
3.4.1 Mathematical Derivation
우선 수학적으로 간단한 모델에 대해서 증명해 보자. 전류에 기여하는 전자의 경우, conduction band에서 자유롭게 이동하지만 결정이 가지는 물리적 크기 내부에 한정(confined)될 것이다. 이를 Particle in a Box 모델로 보자면 3D 무한퍼텐셜 우물구조일 것이다. 간단히 한변의 길이가 a인 정육면체 결정을 생각하자. 이를 식으로 표현하면,

무한퍼텐셜 우물(Infinite potential well)에서의 파동함수를 정리할 때, 다음과 같은 식을 배웠다.
$$ \psi(x)=\sqrt{\frac{2}{a}}\mathrm{sin}(\frac{n\pi x}{a}), k_{n}=\frac{2mE_n}{\hbar}=(\frac{n\pi}{a})^2 \therefore E_n=\frac{\hbar^2n^2\pi^2}{2ma^2} $$
(물리전자개론#2-2 Introduction to Quantum Mechanics 참고)
이를 (변수분리가 가능하다는 가정 하에) 3차원으로 확장하면 밑의 식처럼 쓸 수 있고 그림으로 표현하면 다음 그림과 같다. (식의 형태가 3차원상에서의 거리 구하는 공식과 동일하기 때문에 그림처럼 표현 가능)


[# of states]
2D 에서 먼저 가능한 quantum states를 보자면, 임의의 k에 대해서 k~k+dk 구간의 원형 띠가 될 것이다. 3D에선 k~k+dk 구간의 구각에 동일하게 적용하면 될 것이다. 다만 양자수는 모두 양수이므로 1사분면에 한정된다. 따라서 해당 영역은 \( \frac{1}{8}4\pi k^2dk \)가 된다. 마지막으로 각 전자는 spin이 두개 존재하므로 2를 곱해줘야한다: \( 2(\frac{1}{8})4\pi k^2dk \)
[per Volume]
state의 부피를 구하기 위해서는 각 축마다 k간 거리를 곱해주면 될 것이다. 각 축에서 k와 k+dk의 거리는 k의 양자화로 인해 다음식과 같이 \( \frac{\pi}{a} \)이다.

따라서, 부피는 각 축의 dk를 곱한 것이므로 \( (\frac{\pi}{a})^3 \)이 된다.
k-space에서 상태들의 밀도를 구해보자. k-states 밀도를 임의로 \(g_T(k)dk\)라고 하면 다음과 같다.

(여기서 2는 전자의 스핀, 1/8은 주양자수가 양수인 부분으로 8분면중 1분면을 의미한다.)
우리는 전자의 k보다는 E를 접하기 더 쉬울 것이다. 따라서 dk 가 아닌 dE로 변환하고 싶다. \( k^2 = \frac{2mE}{\hbar^2} \)이므로 양변을 미분하면 dk와 dE의 관계식을 얻을 수 있다: \( dk=\frac{1}{\hbar}\sqrt{\frac{m}{2E}}dE \)
이 식을 위 부피밀도 식에 대입한 후 정리하게 되면 다음과 같은 식을 얻을 수 있다.

기존의 식이 k-space 상에서\( a^3\) 결정 내의 k~k+dk 에 해당하는 상태밀도였다면 변환된 식은 real space에서 \( a^3\) 결정 내의 E~E+dE에 해당하는 상태 밀도를 의미하게 된다.
우리는 어느 영역에서나 적용할 수 있게 단위 부피와 단위 에너지에 대한 상태밀도를 알아보려한다. 단위 부피를 위해 양 변을 결정 부피인 \( a^3\)로 나누고, 단위 에너지를 위해 dE로 나누면 다음과 같은 식이 나오는데 이를 Density of State라고 정의한다.

-(추가) 1D, 2D 에서의 DOS
우리는 3차원에서 살고 있지만 모든 물질이 3D처럼 행동하는 것은 아니다. 한 차원 또는 두 차원을 극단적으로 줄이게 되면 그 물질은 2D 또는 1D 처럼 행동할 것이다. (A4 종이나 실을 생각해 보자)
실제 반도체 물질이 2D 또는 1D 처럼 행동하면 양자효과 때문에 특수한 성질을 띄게 된다. 이를 활용해서 다양한 기능을 구현할 수 있기 때문에 일부 물질은 의도적으로 2D 또는 1D로 구현한다. 이를 Quantum well, Quantum wire이라고 하고 대표적인 예시로 hBN이나 그래핀, CNT등이 대표적인 예시다. 최근에는 0D 물질의 응용으로 display에 적용되고 있는 Quantum dot 퀀텀닷 기술등이 있다.
이 경우에도 carrier density를 구해야 하므로 동일한 방식으로 DOS를 구할 수 있다. 3D와 2D, 1D의 차이점들만 적용하자. 우선 k-space의 volume이 달라진다 : 1D는 \( (\frac{\pi}{a})\), 2D는 \( (\frac{\pi}{a})^2 \)
다음으로 # of state가 달라진다. 3D 환경에서는 구각 영역이었지만 2D에서는 원형 띠 \( 2\pi kdk \), 1D에서는 직선(dk)이 될 것이다.
이들을 동일한 방식으로 적용하여 각 차원에 대해 DOS를 구하면 다음과 같은 결과가 나온다.


3.4.2 Extension to Semiconductors
이때까지 3D 무한퍼텐셜 우물에 있는 자유전자에 대한 DOS를 구하였다. 이제 반도체로 확장해서 conduction band의 전자와 valance band의 정공에 대해 DOS를 구해보자.

k=0 부근에서 E-k 곡선은 포물선에 근사할 수 있다. 이를 식으로 표현하면,


\(E_c\)는 극점에서의 E, \((m_n)^* \)는 전자의 유효질량을 의미한다. 아래의 식처럼 정리하게 되면, 극점 근처에서 전자는 질량만 유효 질량으로 바뀔 뿐 자유전자처럼 행동하는 것을 의미한다. 따라서 위에서 구했던 자유전자에 대한 DOS식을 이용할 수 있다. 다만 에너지만 \( E - E_c \)로 바뀐다. 따라서 conduction band에서의 전자는 다음과 같이 일반화(generalize)할 수 있다.

동일한 방법으로, valance band의 정공에도 적용할 수 있다. 다만 질량이 정공의 유효질량으로 바뀌고 E도 \( E_v - E \)로 바뀐다.

위 두식을 하나의 그래프로 표현하면 다음과 같이 그릴 수 있다. \(E_c\)와 \(E_v\)의 차이는 energy gap이다.

이렇게 반도체에서의 DOS를 구해보았다. DOS는 상태'밀도' 함수이므로 상태 수를 구하기 위해서는 해당 에너지, 또는 부피에 대해서 적분하면 구할 수 있다.
(DOS 유도 참고영상)
https://www.youtube.com/watch?v=SA4xekzUiiM&t=869s
3.5 | STATISTICAL MECHANICS (통계 역학)
우리가 풍선의 압력을 구한다고 생각해보자. 그러면 우리는 풍선 내부의 모든 공기에 대해 고려하는 것이 아닌, 풍선의 벽면에서 때리는 공기들만 고려하면 될 것이다. 이처럼 반도체 역시 수많은 전자가 있기에 모든 전자의 상태를 알아보는 것은 비효율적이다. 따라서 우리는 이제 전기적 특성에 관여하는 전자,정공들에 대해서만 행동을 관찰할 것이다.
3.5.1 Statistical Laws
1.맥스웰-볼츠만 확률함수(Maxwell–Boltzmann probability function) (거시)
2.보스-아인슈타인 함수(Bose–Einstein function) (보손)
3.페르미-디락 확률함수(Fermi–Dirac probability function) (페르미온)
우리는 입자의 행동을 알아보기 위해 통계역학을 지배하는 3가지 분포함수에 대해 배울 것이다. 각자 입자의 특성에 따라 적용되는 것이기에 우리는 입자의 종류부터 간단히 알아보자.
- 거시 vs 미시, 페르미온 vs 보손
[거시세계]
우선 우리가 살고 있는 거시세계를 보자. 고전역학이 지배하고 있는 거시세계에서 입자는 우리가 하나씩 셀 수 가 있다. 이 입자들은 같은 에너지 상태를 가지는 입자가 있어도 상관이 없다. 공기 중 산소를 생각해보자. 산소분자들은 (많긴 하겠지만)하나씩 셀 수 있으며 같은 에너지 상태를 갖는 산소분자가 2개이상 존재할 수도 있을 것이다.
[미시세계]
반면 미시세계는 고전역학이 아닌 양자역학이 지배하고 있다. 미시세계에서는 양자역학 특성상 입자들을 하나하나씩 구분할 수 가 없다. 여기서는 입자의 종류가 2가지가 존재한다 : 페르미온, 보손
[보손]
보손(Boson)이라고 불리는 입자는 2가지 특성이 있다. 1.구분이 불가능하다. 2.같은 에너지상태를 가질 수 있다. 거시세계의 산소처럼 같은 에너지 상태를 가지는 입자가 2개이상 존재할 수 있지만, 보손의 경우 그 입자들을 구분할 수 없다(indistinguishable). 대표적인 예시로 광자(photons), 흑체복사가 있다.
[페르미온]
페르미온(Fermion)이라고 불리는 입자도 2가지 특성이 있다. 1.구분이 불가능하다. 2.같은 에너지상태를 가질 수 없다. 거시세계의 산소분자와 반대된다고 생각하면 된다. 대표적인 예시로 우리가 다룰 전자, 정공등이 있다.
거시세계에서는 맥스웰-볼츠만 함수가 지배적이다. 미시세계로 넘어가서는, 보손에 대해서는 보스-아인슈타인 함수가 지배적이고 페르미온에 대해서는 페르미-디락 함수가 지배적이다. 우리가 다룰 전자의 경우 페르미온에 속하므로 페르미-디락 분포함수에 대해 알아보자.
3.5.2 The Fermi–Dirac Probability Function
-페르미-디락 분포 함수의 개요 (선택)
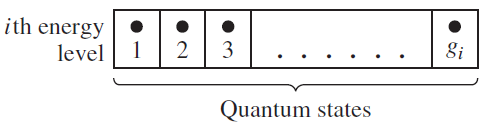
어떤 i번째 에너지 레벨에 존재하는 quantum states를 보자. 가능한 quantum states의 갯수는 1,2,...,\(g_i\)개라고 하자. 이때 전자가 \(N_i\)(<\(g_i\))개가 있다고 할 때, 이 전자들이 가질 수 있는 분포의 가짓수는 몇가지인가?
단순히 방 \(g_i\)개에 공 \(N_i\)개를 배치하는 단순 조합문제이다. 전자는 페르미온이므로 서로 구분할 수 없으니 combination을 사용하면 될 것이다. 따라서 가능한 전자의 분포 가짓수 \(W_i\)는 \(g_iC_N\) 또는,
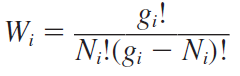
i번째 에너지 레벨에 대한 전자들만 적용한 결과이다. 그렇다면 결정 전체 전자에 대해 적용하자면 전자의 전체 분포 가짓수는 각 에너지 레벨의 분포 가짓수를 곱한 다음과 같다.
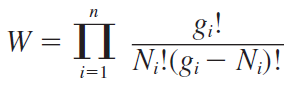
우린 이중에서 가장 가능성이 높은 분포를 찾고 싶다. 전자의 개수, 에너지 레벨 등에 따라 분포 함수 W는 달라질 것이다. 이때 가장 확률이 높은 분포 함수는 다음과 같다.
페르미 디락 함수 \(f_F(E)\)는 다음과 같다.

N(E)는 입자의 부피,에너지당 밀도함수 이며 g(E)는 상태밀도 함수이다. 이 함수가 가지는 의미는 에너지 E가 주어졌을 때, 전자가 존재할 확률을 의미한다. \(E_F \)는 페르미 에너지 레벨로 전자가 존재할 확률이 0.5인 에너지 레벨을 의미한다. 이 페르미 에너지 레벨은 나중에 에너지의 기준값으로 활용된다.
3.5.3 The Distribution Function and the Fermi Energy
식을 간단히 해석해보자.
1. T=0K
온도가 0K이면 모든 전자는 안정화되어 각 states에 차있을 것이다. 식에서의 exp항이 무한히 작아지므로 값은 0에 수렴할 것이고 \(f_F(E) =1\)이 된다. 그림으로 나타내면 다음과 같다. 이때 전자는 페르미 에너지 레벨까지 모두 차있게 된다.

2. E → \(\infty\)
에너지가 과할 경우 모든 전자는 여기된 상태일 것이다. (states에 차있지 않을 것이다.) 식으로 보면 exp항이 무한대로 발산하므로 \(f_F(E) =0\)이 된다.
E가 무한히 가지 않아도 페르미 레벨보다 적당히만 커도 exp항으로 분모가 커지게 되므로 \(f_F(E) \)은 0에 수렴할 것이다.
3.T >0K
T=0K일 때는 페르미 레벨까지 모두 1이지만 T>0K 인 경우에는 그래프가 \(E_F\)기준으로 넓게 퍼지게 된다. 다만 여전히 \(E_F\)를 지날때 확률은 0.5이다. 온도가 높을 수록 \(E_F\)를 넘어서는 입자의 갯수가 늘어남을 알 수 있다.

전자만 고려했는데 정공도 고려해야 하지 않는가? 라는 질문이 생길 수도 있다. 하지만 정공의 경우 전자의 빈자리이기 때문에 위 함수를 1에서 뺀 값이 정공에 대한 페르미-디락 분포가 된다. 이를 그래프로 같이 나타내보면 다음과 같다.

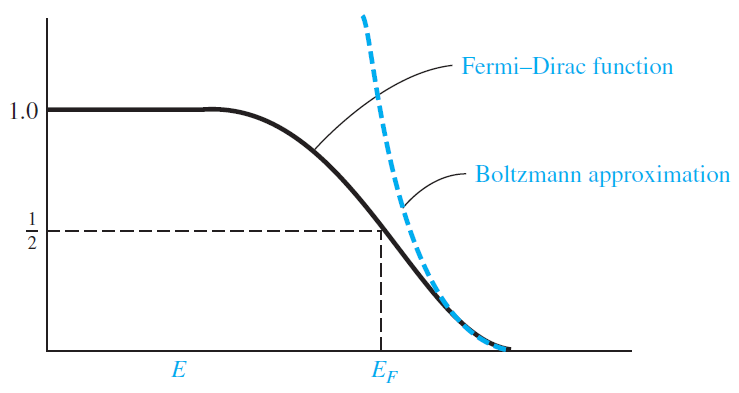
-(볼츠만 근사)
E가 적당히 높아 kT 값보다 매우 클 경우 볼츠만 곡선과 매우 유사하여 근사를 사용할 수 있다. 이경우 페르미 디락함수의 분모에서 1을 생략할 수 있다. 따라서 식의 형태는 다음과 같이 근사할 수 있고 이는 볼츠만 함수 형태이다.
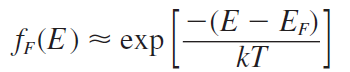
이렇게 3단원이 마무리 되었다.
3단원에서는 앞으로 배울 전자 밀도를 구하기 위한 기초지식을 배웠다. 전자의 에너지레벨, Band theory, kp model, 전자-정공, 유효질량, 상태밀도함수 그리고 페르미 디락 분포함수까지.
개인적으로는 E-k diagram을 보는 법을 익혔으면 좋겠고 Band theory와 DOS의 개념정도 확실히 하고 넘어가면 앞으로 큰 문제는 없을 것이라고 생각한다.(kp model의 증명까지는 아직 필요없다고 생각한다)
다음글:
물리전자개론#4-1 The Semiconductor in Equilibrium
물리전자개론#4-1 The Semiconductor in Equilibrium
4.0 | PREVIEW In this chapter, we will: ■ Derive the thermal-equilibrium concentrations of electrons and holes in a semiconductor as a function of the Fermi energy level. ■ Discuss the process by which the properties of a semiconductor material can be
cucudasdiary.tistory.com
이전글:
물리전자개론#3-2 Introduction to the Quantum Theory of Solids(E-k 그래프, 전류, 유효질량,정공,도체/반도체/부도체 구분)
물리전자개론#3-2 Introduction to the QuantumTheory of Solids
3.2 | ELECTRICAL CONDUCTION IN SOLIDS 우리는 기본적으로 반도체 물질에서의 전류-전압특성을 알아보는 것이 목표이다. 따라서 이전 강의에서 배웠던 Band theory를 사용하여 전자의 움직임 부터 알아볼 것
cucudasdiary.tistory.com




