물리전자개론 #6-3 켤례전하 전송방정식, 확산계수, 이동도, carrier 농도 그래프

 

 

6.3 | 켤례전하 전송(AMBIPOLAR TRANSPORT)

균일하게 도핑된 반도체의 중성영역에서 과잉 캐리어 농도의 공간적 분포와 시간에 따른 변화는 켤례전하 전송방정식에 의해 지배된다 : 과잉 캐리어의 공간적,시간적 변화는 캐리어의 유입-유출과 생성-재결합에 의해 결정된다.

 이제 이상적인 반도체에서 실제 반도체 모델로 넘어가면서 요소들을 하나씩 바꾸고 있다. 아까는 외부 요인에 의한 과잉캐리어 (excess carrier)에 대해 다뤘는데, 이번에는 전기장을 실제 상황에서의 전기장으로 바꿀 것이다.
 이때까지는 외부에서 걸어준 전기장(E-field)만 고려했다. 하지만 외부 전기장\(E_{app}\)이 가해지면 내부에서는 과잉 캐리어가 생성될 것이고 이렇게 특정 공간에 생긴 과잉 캐리어들은 전하의 불균형을 초래하여 내부 전기장\( E_{int} \)을 형성한다. 

그림 1. 1차원에서 내부전기장

즉, 위와 같은 형태가 된다. 따라서 반도체에 걸리는 총 전기장은 외부전기장\(E_{app}\)과 내부전기장\( E_{int}\) 총합이며 식으로 나타내면,

외부적인 요소에 의해 생성되는 과잉 캐리어들은 항상 홀-전자 쌍으로 생성되며 내부 전기장을 형성한 상태로 이동한다. 즉, 생성된 과잉 전자와 과잉 홀들은 '같이' drift되거나 diffusion되며 하나의 이동도(mobility)와 확산계수(diffuision coeff)를 가지게 된다. 이러한 현상을 켤레전하 전송(ambipolar transport)라고 한다. 이러한 켤레전하를 지배하는 이동방정식을 알아 볼 것이다.

---

6.3.1 중성영역에서의 켤례전하 전송방정식 유도

이제 내부전기장에 의한 excess carrier들의 변화를 알아보자.
미적분학 시간때 라플라스 방정식을 배웠고 이를 바탕으로 전자기학 시간때 푸아송 방정식을 배웠을 것이다. 
$$ \bigtriangledown V= -E $$
$$\bigtriangledown E=\frac{\rho}{\epsilon_0} $$
$$\bigtriangledown^2 V= -\frac{\rho}{\epsilon_0} $$

이를 그림.1에 적용해보자. 전기장 \(E\)는 내부전기장 \(E_{int}\)로, 전하밀도 \(\rho\)는 excess carrier의 합인 \(\delta p - \delta n\)이 될 것이다.

아니 근데 주인장, 방금 "중성영역"이라고 했지 않았는가? 바로 위에서 excess carrier로 인한 전하 불균형에 의해 내부전기장 \(E_{int}\)가 생성된다고 했는데 중성영역에서 어떻게 전기장 \(E_{int}\)을 취급할 수 있단 말인가?

라는 의문을 가질 수도 있다. 하지만 "중성영역"이라는 것은 거시적으로 보았을때 전하의 net sum이 0이라는 말이지, 모든 공간에서 전하가 0으로 유지되는 것은 아니다. 국소적인 부분에서는 당연히 모종의 이유로 excess carrier의 불균형이 일어나 carrier의 diff와 drift가 유발되며 이로 인해 충분히 내부전기장 \(E_{int}\)이 생성될 수 있다. 따라서 \(\bigtriangledown E= \bigtriangledown E_{int}\)가 가능하다.

자, 이쯤에서 이전 글에서 배웠던 1차원 시간의존 확산방정식을 다시 한번 꺼내보자.

이 식을 "중성영역"에서의 "켤례전하" 이동방정식으로 만들려고 한다. 그러면 앞의 두 조건 "중성영역"과 "켤례전하"로 인한 것들을 적용시켜보자. 
  1."켤례전하"는 전자와 정공이 서로 쌍으로 움직임을 의미한다. 전자와 정공이 서로 동시에 생성되고 소멸되므로 이는 곧 excess carrier로 생성 또는 재결합되는 전자와 홀의 농도가 동일하여 서로 상쇄됨을 의미한다. ▶\(g_n = g_p = g, R_n=\frac{n}{\tau} =R_p=\frac{p}{\tau} =R\)
  2. "중성영역"은 전하가 0인 영역을 의미한다. 따라서 전자의 농도와 정공의 농도는 서로 비슷하여 전하를 상쇄할 수 있어야 한다. ▶\(\delta n = \delta p\)
이 두 조건을 1차원 시간의존 확산방정식에 넣고 정리하면 다음과 같다.

우리는 carrier에 대한 방정식을 알고 싶은 것이지, 전기장의 변화에 대한 식을 알고 싶지는 않으니까 양변에 적당한 상수를 곱해서  \(\frac{\partial E}{\partial x}{x} \)항을 제거하자. 위 식에는 \(\mu_n n\)를, 아래 식에는 \(\mu_p p\) 을 곱하면 될 것 같다. 식을 정리하면

와 같은 식이 나오고 이를 켤례전하 전송방정식이라고 한다. 식을 살펴보면 excess carrier(전자로 표시되어 있지만 켤례전하이므로 정공도 포함)들의 시간과 공간에 대한 거동을 표현하는 방정식이다. 못보던 \(D' , \mu'\) 상수는 다음을 간략하게 표기한 것이다. 

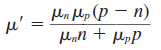
이번 단원 처음에 언급했듯이, 켤례전하는 쌍으로 움직이므로 같은 확산계수와 이동도를 가진다고 하였다. 위의 식들이 그 값에 해당하고 각각 켤례전하 확산계수(D',ambipolar diffusion coefficient), 켤례전하 이동도(\(\mu'\),ambipolar diffusion coefficient)가 된다. 아인슈타인 관계식을 사용하면 D'를 조금더 간결하게 표현 할 수 있다.(\(\frac{\mu_n}{D_n}=\frac{\mu_p}{D_p}=\frac{e}{kT}\))

켤례전하 확산계수

켤례전하 이동도

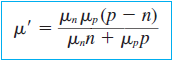
균일하게 도핑된 반도체의 중성영역에서 과잉 캐리어 농도의 공간적 분포와 시간에 따른 변화는 위 식에 의해 지배된다. 과잉 캐리어의 공간적,시간적 변화는 캐리어의 유입-유출과 생성-재결합에 의해 결정된다.

---

6.3.2 Low injection 외인성 반도체에서의 연속방정식

전자와 정공은 반드시 켤례로 움직이며, 뱡향과 속력은 반도체의 소수 캐리어에 의해 결정된다

여태 그랬듯이, Low injection을 가정하고 식을 다시 보자. 즉, 기존의 있던 carrier들에 비해 주입된 carrier들이 매우 적다는 말이다.자 그러면 위에서 구했던 계수들을 다시 구성하여 전송방정식을 유도해보자.

[D']
 carrier의 농도 n과 p를 좀더 풀어서 확산계수를 표현하면 다음과 같다. (Carrier농도= 열평형 carrier 농도 + 과잉 carrier 농도)

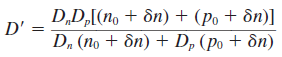
이때, low injection이 아니라 특정 dopant가 다량으로 주입된 n-type 또는 p-type 반도체의 경우를 생각해보자. 
  1. p-type 반도체
\(n_0 << p_0\))(p-type) , \(\delta n << p_0\) (low injection)이므로 \(n_0, \delta n\)항들을 모두 무시하면 확산계수는 \(D'=D_n\)으로 표현할 수 있다.
  2.n-type 반도체 
마찬가지로 \(p_0 << n_0\))(p-type) , \(\delta p << n_0\) (low injection) 조건에 의해 \(D'=D_p\)가 성립한다.

[\(\mu\)]
확산계수 뿐만 아니라 이동도 역시 동일한 방법으로 근사할 수 있다. 이 경우 역시 확산계수때와 동일한 방식으로 진행되며 결과값은 다음과 같다. p-type: \(\mu' = \mu_n\) , n-type: \(\mu' = -\mu_p\) 여기서 n-type 이동도가 음의 값을 가지는 이유는 이동도가 drift 전류와 연관이 있기 때문에 전하의 요소를 고려해서 - 부호가 붙게 된 것이다.

[g,R]
이제 켤례전하 전송방정식에서 남은 항은 g와 R항이다.

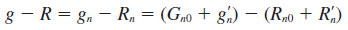
생성(g)은 열평형 상태 carrrier들의 생성(\(G_{n0,p0}\))과 과잉 carrier들의 생성(\(g'_{n,p}\))의 합이고 재결합(R) 역시 열평형 상태의 carrier들의 재결합(\(R_{n0,p0}\))과 과잉 carrier들의 재결합(\(R'_{n,p}\))의 합이다. 여기서 열평형상태에서는 carrier의 변화가 없는 정상상태이므로 열평형 상태에서의 생성률과 재결합률은 같다.((\(G_{n0,p0}=R_{n0,p0}\)) 따라서 과잉 캐리어들에 대한 생성과 재결합만 고려하면 된다.

(p-type 반도체) Low injection에서 majority carrier인 정공들은 이미 수가 압도적으로 많기 때문에 과잉 캐리어에 의한 영향을 무시, 상수로 취급할 수 있다. 그렇다면 재결합률은 소수 캐리어인 전자의 농도에 의해 결정 될 것이다. 따라서 재결합률은  \( \frac{\delta n}{\tau_n}\)으로 표현할 수 있다. 이들을 모두 고려하면 g와 R항은 다음과 같이 표현된다.

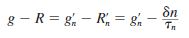
이렇게 구한 계수들을 위에서 구한 전송방정식에 대입하면 Low-injection에서 외인성 반도체의 켤례전하 전송방정식은 다음과 같다.

p-type, 전자에 의해 결정

n-type, 정공에 의해 결정

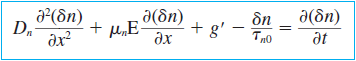
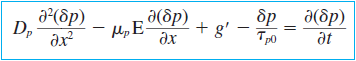
외인성 반도체 내부 켤례전하는 minority carrier에 의해 결정됨을 알 수 있다. 이는 앞으로 반도체 소자의 특성과 행동을 설명할때 굉장히 중요한 기초지식이 된다.

위 전송방정식은 상황에 따라 어떤 효과를 가지는지 알아야 한다. 대표적인 상황에 대한 전송방정식 결과는 아래 표와 같다. 해당 조건에 맞게 식을 대입하여 미분방정식을 해결하면 excess carrier의 시간(또는 거리)에 대한 함수를 구할 수 있을 것이다.

균일하게 도핑되어 있고(조건2) 과잉 캐리어들의 생성을 무시(조건3)한다면 minority carrier의 시간에 대한 1차 미분방정식만 남게되어 다음과 같은 함수를 얻을 수 있다.

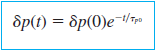
또는, 위에서 생성까지 고려하여 미분방정식을 풀면,

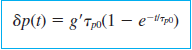
이렇게 생성된 과잉 캐리어에 의해 균일하게 도핑되었다는 조건이 깨지면 특정 시간에 대해 거리에 대한 함수도 구할 수 있다. 추가적인 생성은 없다고만 가정하자, 그러면

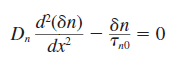
이런 미분방정식을 풀어

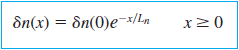
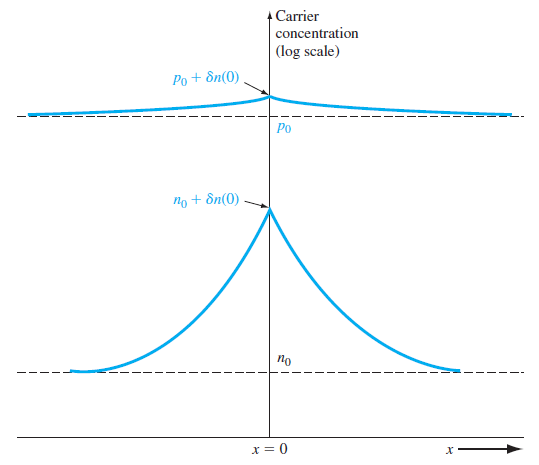
이와 같은 결과가 나오고 이를 그래프로 표현하면 생성 지점을 기준으로 exp함수에 맞게 그려진다.

여기서 외부 전기장까지 고려하게 된다면 carrier들의 시간에 따른 움직임도 표현하여야 한다.따라서 다음과 같은 미분방정식을 풀어야 한다.

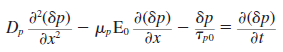
얘를 풀면 과잉 캐리어는 시간,거리에대한 함수로 나오는데,

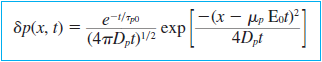
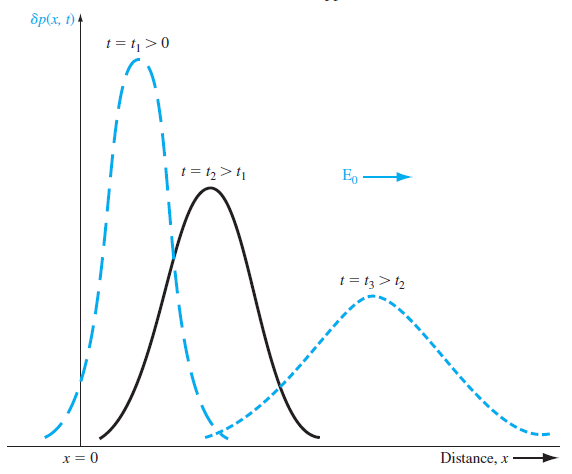
이를 그래프로 표현하게 되면 다음과 같다.