| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 반도체 이론
- 전자농도
- 맛집
- 공간 전하 영역
- SVP
- 물리전자개론
- minority carrier
- 과잉캐리어
- 반도체이론
- PN diode
- 삼성전자DS
- 홀
- DEPLETION REGION
- 무한리필
- PN junction
- 삼성면접
- 공핍영역 넓이
- pn접합
- 삼성전자
- Lifetime
- 반도체연구소
- EE204
- 반도체 소자
- 반도체
- 취업준비
- 점진적 도핑
- 당일치기
- 반도체소자
- 공핍영역
- 합격후기
- Today
- Total
쿠크다스 멜랑쥬
반도체소자 #8-1 PN접합 다이오드, IV 특성, 순전압에서의 carrier 농도 본문
Chapter 8. PN Junction Diode
이전 단원에서는 '열평형'과 '역전압'상태에서의 PN접합 - 에너지밴드, Built-in potential barrier, 공핍영역과 전기장에 대해 알아보았다. 이번 단원에서는 역전압이 아닌, '순전압'에서 PN접합과 'I-V 특성'에 대해 알아볼 것이다.
[8.0 Preview]
■ PN 다이오드에 순접압이 걸리는 상황에 대해 알아볼 것이다 - 전기장, 전위, carrier움직임 등
■ 순전압이 걸리는 상황에서 excess minority carrier의 거동에 대해 알아 볼 것이다
■ I-V 특성 그래프를 그려볼 것이다
■ 지금까지의 가정 - Low level injection이 아닌 비이상적인 상황(non-ideal effect)에 대해 다루어 볼 것이다.
ex) high level injection, generation/recombination(생성/재결합)
■ 소신호 회로에 대해 알아볼 것이다
■ 터널링 현상과 터널 다이오드(tunnel diode)에 대해 알아볼 것이다.
[8.1 PN 접합 전류 @순전압 (PN JUNCTION CURRENT @ FORWARD BIAS)]
8.1.1 pn접합에서 charge flow에 대한 정성적 설명
PN 접합에 역전압을 걸었을때 변화는 알아보았으니 이제 순접압을 걸어보자. P-side에 (+)전압을, N-side에 (-)전압을 걸면 결론적으로 전류가 흐르게 된다. 이 이유에 대해 먼저 간단하게 알아보자.

1.(+)전압을 걸어주면 Fermi level은 낮아지고 (-)전압을 걸면 Fermi level은 높아진다.(Fermi level은 '전자'의 에너지 양이라고 생각하면 (-)전압은 전자의 에너지를 높여주는 방향이기 때문에 Fermi level이 높아지는 것은 자명하다)
2. p-region과 n-region의 energy band 차이가 줄어들고 이는 곧 potential barrier의 감소를 의미한다(순전압 만큼).
3. 이는 carrier의 이동을 막는 공핍영역의 전기장의 세기가 줄어들었다는 의미이며, 해당 barrier보다 더 큰 에너지를 갖는 carrier들은 barrier를 넘어 전압의 방향대로 흐르게 된다 (n-region 전자 -> p-region (+) / p-region 정공 -> n-region(-))
8.1.2 이상적인 전류-전압 관계식 (Ideal Current-Voltage Relationship)
전류가 흐르는 정성적인 해석은 했으므로 이제 전류가 정확히 어떻게 흐르는지 알아보고 싶다. 하지만 처음부터 실제상황을 가정하면 너무 복잡해지기 때문에 우선 '이상적인 상황'을 가정하자. (이전 단원에서 했던 가정들과 동일하지만 전류 관련 가정이 하나 추가되었다)
1. 공핍영역은 중성영역과 abrupt한 경계를 갖는다. (carrier의 농도같은 것들이 step function 형태를 갖는다)
2. carrier들의 움직임은 Maxwell-Boltzman 근사가 적용된다. (이전 글 참고:물리전자개론#3-3)
물리전자개론#3-3 Introduction to the Quantum Theory of Solids(Density of states at 1D/2D/3D, 통계역학,페르미-디락
3.4 | DENSITY OF STATES FUNCTION 우리는 전류 전압특성을 다루기 위해 우선 전하를 가지는 입자들의 분포(charge carrier distribution), 또는 전자와 정공의 분포를 알고 싶다. 이를 알기 위해서는 Density of State
cucudasdiary.tistory.com
3. low level injection 그리고 completely ionization (적은 양의 dopant만 주입되고 해당 dopant들은 100% 이온화)
4A. 전류의 크기는 PN접합에서 모두 동일하다
4B. 전자와 정공의 전류는 PN접합에서 연속적이다
4C. 전자와 정공의 전류는 공핍영역에서 일정하다
이제 전류식을 유도할 것인데 굉장히 기호가 굉장히 헷갈리게 사용되므로 먼저 알아보고 가자.

우선 기호 n과 p는 각각 전자와 정공을 의미한다. 문제는 밑첨자들인데 n이면 n-region, p이면 p-region이고 0이 추가로 붙어있으면 열평형상태를 의미한다. 이 기호들을 충분히 눈에 익혔으면 전류식을 유도해보자.
8.1.3 순전압에서 Carrier 농도 - 경계조건 (Boundary condition)

위 그림과 같이 PN접합에 순전압 Va만큼 걸어준 상황을 가정하자. (Low injection 가정하에) carrier의 농도는 어떻게 될까?
먼저 7단원에서 PN접합에서 Built-in poteintial은 다음과 같이 표현할 수 있다고 배웠다.(여기서 \(V_t = kT/e \))
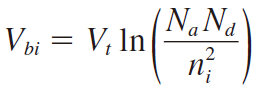
양변을 \(V_t\)로 나누고 exp를 취해주면,

위 식을 전자에 대해 서술하고 싶다. 우리는 기본적으로 1.low injection 2.fully ionization 3.thermally equilibrium 상황을 가정한 상태이다. 따라서 N영역에서 \(N_d=n_{n0}\) 가정이 성립한다. 동일한 방법으로 P영역에서도 \(N_d=p_{p0}\)가 성립한다. 다만 우리는 전자에 대해서만 먼저 볼 것이기 때문에 P영역의 전자에 대한 식으로 바꿔줄 것이다. 이전에 열평형상태에서는 항상 \(N_aN_d=n_i^2\) 가 성립함을 배웠다. 따라서 \(n_{p0} \approx \frac{n_i^2}{N_a} \) 가 성립하게 된다. 해당 식들을 위 식에 대입하면,
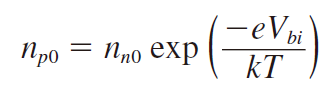
P영역의 전자(minority carrier)와 N영역의 전자(majority carrier)의 관계식을 도출해낼 수 있다. (정공에 대해서도 동일한 식이 성립한다) 열평형 상태에서 식을 알아봤으니 순전압을 가했을때도 알아보자.

순전압을 가해주면 \(V_{bi}\)가 감소하고 exp항의 값은 증가하여 결국 P영역의 전자의 농도도 높아지게 된다 == 전류가 더 잘 통하게 된다. 우변의 exp항을 잘 나눠주면 열평형상태의 전자농도와 나머지 exp항으로 구성되어있음을 알 수 있다. 식을 좀 더 간편히 표현하면,


PN접합에서 Doping농도를 알면 각 영역에서 열평형 상태에서의 carrier농도는 알 수 있다(\(n_{p0}, p_{n0}\)). 따라서 PN접합에 가해진 전압의 크기만 알면 각 영역의 carrier농도를 알 수 있다. (\(\np=n_i^2\))
위 식을 그래프로 표현하면 다음과 같다.

순전압이 가해졌을때 열평형상태일때 보다(점선) excess minority carrier들이 생성됨을 알 수 있다. 다만 이 농도는 공핍영역 가장자리지점에 대해서만 해당하는 값이다. 공식유도를 공핍영역에서의 Built-in potential에서 시작하였기 때문이다.
8.1.4 중성영역으로의 소수 캐리어 분포 (Minority carrier distribution)
아까까지 공핍영역 가장자리에서의 minority carrier 농도를 알아보았다. 이제 중성영역에서의 carrier 농도가 어떻게 분포될 것인지 알아볼 것이다. 처음부터 1D 상황을 가정했으므로 1D에서 carrier 거동을 설명하는 켤례전하 전송방정식을 살펴보자.

식의 간편화를 위해 캐리어의 생성(generation)은 없다고 가정하고(g'=0) 중성영역이므로 전기장 또한 0이 된다. 따라서 식은 다음과 같이 간편화 된다. 여기서 \(L^2 = D_p\tau_{p0}\)

2차 선형 미분방정식이므로 경계조건을 찾아야한다.
1.공핍영역 가장자리에서의 농도는 위에서 구한 값이다.
2.중성영역의 무한대 지점에서의 농도는 열평형상태의 값고 동일하다.
이를 식으로 나타내면,

2차 선형 미분방정식의 일반해의 형태는 \(y=c_1e^{r_1t}+c_2e^{r_2t} \) 이다. 여기서 경계조건을 활용해서 식을 풀면 excess carrier 농도에 대한 식을 구할 수 있다.


식은 '과잉'캐리어들에 대한 식임을 인지해야 한다. 식을 자세히 살펴보면 \(n_{p0}[exp-1]\)항은 상수임을 알 수 있다. 따라서 거리가 공핍영역으로부터 멀어짐에 따라 exp하게 감소함을 알 수 있다. 이를 그래프로 나타내보면 다음과 같다.

그렇다면 특정 지점에서의 캐리어 농도는 어떻게 구할 수 있을까?
우리는 6단원에서 quasi-Fermi level을 배웠다. 쉽게말해, 비평형상태에서 각 캐리어가 fermi-level을 갖는 것을 말한다. 이상황에서도 순전압(forward bias)가 계속 흘러 quasi-Fermi level을 가정하면 energy band는 다음과 같다.

여기서 각 캐리어 농도는 intrinsic한 캐리어 농도에서 intrinsic Fermi level과 quasi-Fermi level의 차이의 exp을 취한 값의 곱임을 배웠다.


위 식에 따라 P쪽의 공핍영역 근처에서 보면 전자의 페르미 레벨 역시 intrinsic한 페르미 레벨보다 높으므로 과잉 전자가 존재한다. 여기서 공핍영역으로 부터 거리가 멀어질 수록 감소하게 된다. 그리고 우리는 그 감소율이 exp하다는 것을 이때까지 알아봤다.
마지막으로 임의의 지점에서 두 캐리어의 농도를 곱해보자. 분명 열평형 상태에서는 np곱은 \(n_i^2\)임을 배웠다. 그렇다면 quasi-Fermi level에서는 어떻게 되는지 알아보자. 바로 위 두 식을 곱해보면,

임을 알 수 있다. bias가 가해진 상태에서 두 quasi-Fermi level의 차이는 가해준 bias의 크기와 상관있으며, 특히 공핍영역에서의 np곱은 bias에 exp하게 비례함을 알 수 있다.
다음글:
이전글:
반도체소자 #7-3 Junction Breakdown,점진적 도핑 접합, 초계단 접합, varactor diode
[7.4 Junction Breakdown] 요 내용은 8장 PN 접합에서의 전류를 배우고 나서 다시 할 예정이다. 간단하게 말하면 PN 접합에서 역전압을 걸어주었을때 전류가 통하는 상황을 의미하며 1.(Zener)고농도 도핑
cucudasdiary.tistory.com



